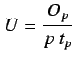6.2 MODELIZACIÓN MATEMÁTICA DE PROCEDIMIENTOS

Formalización de recursos. Objectivo de rendimento

La formalización de los recursos que posee cada nodo permitirá construir una visión general del funcionamiento de ponderación de tales recursos dentro del cluster. La nomenclatura a partir de ahora utilizada identificará

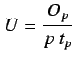• el conjunto de $n$ nodos que conforman el cluster.

Luego los $m$ recursos que posee un nodo $i_k$ cualquiera se identificaran por el conjunto $R(i_k)$ de esta forma:

• $R(i_k) = \{ r_c(i_k),\ r_m(i_k),\ ...\ \},\ \ 1\leq k\leq n\ \ \equiv$ conjunto de recursos del nodo $i_k$ .
• $\vert R(i_k)\vert=m$ .

Esto permite ver a cada nodo como un cúmulo de recursos, dispuestos para ser utilizados por el cluster. por lo tanto, extrapolando conceptos, un cluster no deja de ser también una conjunción de recursos, así

• $R(I) = \{R(i_1)\ \wedge\ R(i_2)\ \wedge\ ...\ \wedge\ R(i_n) \} = \{\ \{r_c(i_... ...\ r_m(i_2),\ ...\ \}\ \wedge\ ...\ \wedge\ \{r_c(i_n),\ r_m(i_n),\ ...\ \}\ \}$

Un nodo puede tener muchos recursos a la vez: procesador, memoria, targetas PCI, dispositivos de E/S, etc.. Sin embargo no es ahora tan importante saber cuantos recursos gestiona openMosix sino cómo lo hace. Esto es, ¿cómo se llega a la ponderación de cada nodo?

Antes de responder es importante apuntar lo que debiera haberse comprendido en la sección anterior: openMosix basa sus decisiones de migración en una algorítmica basada en modelos económicos, donde los recursos estan ponderados en una misma escala para simplificar los cálculos. Estos cálculos deben ser computables en el menor intervalo de tiempo posible para dotar al sistema de la máxima adaptabilidad a las condiciones cambiantes que los usuarios -los procesos en última instancia- puedan propiciar.

No se entrará -por el momento- en averiguar cómo se equiparan parámetros tan dispares como velocidad de procesamiento o cantidad de memoria. Lo relevante ahora es ver qué permite hacer esta asignación. Se supondrá, para cualquier nodo $i$:

• $$r_c(i_k),\ c\ \epsilon\ R(i_k) \equiv$$ velocidad de procesador de $i_k$ ,

• $$r_m(i_k),\ m\ \epsilon\ R(i_k) \equiv$$ tamaño de memoria de $i_k$ .

Igualmente interesa poder estimar los recursos que necesitarán las distintas tareas $j$, de cara a predecir el nodo donde se ejecutarían con más celeridad. Así se definen para las tareas cuatro parámetros.

• $a(j,i_k) \equiv$ tiempo de llegada de la tarea $j$ en el nodo $i_k$ ,
• $c(j,i_k) \equiv$ tiempo de procesador estimado necesario para la ejecución,
• $m(j,i_k) \equiv$ cantidad de memoria necesaria,
• $T(j,i_k) \equiv$ tiempo real invertido en la finalización de la ejecución.

Se asume, para una algorítmica no ideal -y por tanto suponiéndose implementable- que $m(j,i_k)$ y $c(j,i_k)$ son conocidos y $T(j,i_k)$ es desconocido en $a(j,i_k)$.

La finalidad de la definición de los parámetros que hasta ahora se han visto es poder decidir diversos aspectos que conciernen a la migración de procesos -en última instancia, el objetivo de openMosix-: decisiones sobre qué proceso migrar y dónde hacerlo se apoyan precisamente en los parámetros vistos. Esto es, para definir qué proceso deberá migrarse deben medirse los recursos -y la cantidad de ellos- que ocupará en el nodo que lo hospede. Igualmente para saber qué nodo es el mejor para aceptar dicho proceso deberá medirse la carga computacional de un cierto número de ellos para saber cual dispone de mayor cantidad de ella y, en consecuencia, cual será capaz de retornar el resultado de proceso en el menor tiempo posible.

El poder computacional de un nodo queda definido no solamente por la ponderación de sus recursos, sino por la utilización de ellos tanto en el actual instante como en el futuro que venga marcado por la planificación de tal recurso.

Debería definirse la carga de un nodo. Esto es para un nodo $i_k$ en el instante $t$:

• $J(t,i_k)\ \in\ \mathbb{N} \equiv$ procesos en ejecución,
• $carga_c(t,i_k) \propto J(t,i_k)\ \equiv$ carga de procesador ( $\in\ \mathbb{Z}^+$) ,
• $carga_m(t,i_k) = \displaystyle\sum_{j\ \epsilon\ J(t,i_k)} m(j)\ \equiv$ carga de memoria ( $\in\ \mathbb{Z}^+$).
• $LOAD=\displaystyle\sum \left[ carga_c(t,i_k) + carga_m(t,i_k)\right],\ \forall\ i_k\ \in\ I \equiv$ es la carga total en el sistema en el instante $t$ .

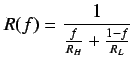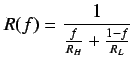Análogamente, la carga de un nodo se mide en función de los recursos de que ya no dispone. En este caso se han dado las expresiones para procesador y memoria.

No obstante para medir la carga de un nodo openMosix no utiliza solamente esta aproximación. Hay condiciones que pueden desajustar notablemente los valores para la carga calculada y la carga real, mayormente cuando el nodo hace swapping.

La implemenación de openMosix soluciona este apartado sirviéndose de un parámetro 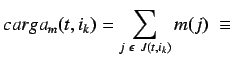$s$, que se convertirá en un factor que multiplicará a la expresión de carga del nodo y que por tanto sobredimensionará el valor calculado tras el repaso de la ponderación de recursos. Esto tiene una completa lógica ya que con acceso a swap el procesador tiene que utilizar muchos más ciclos que trabajando con memoria, para recuperar una página.

Para formalizar esta idea puede escribirse:

• si $carga_m(t,i_k) \leq r_m(i_k) \Longrightarrow carga_c(t,i_k) = J(t,i_k)$ ,
• si $carga_m(t,i_k) > r_m(i_k) \Longrightarrow carga_c(t,i_k) = J(t,i_k)*s$ .

OBJETIVO DE RENDIMIENTO DE OPENMOSIX

El objetivo de los cálculos de openMosix es optimizar el aprovechamiento de la totalidad de los recursos del sistema. Así por ejemplo, para cada nuevo proceso iniciado no se estudia solamente el aumento de carga en el nodo local, sino que se tiene en cuenta el contexto de carga de todo el sistema. Cuando existen suficientes procesadores en el cluster para encargarse de su carga, cada proceso se servirá al procesador menos cargado y se devolverá la respuesta tan rápido como pueda hacerlo.

Si por el contrario no existen suficientes procesadores para encargarse de los procesos pendientes de ejecución, se evaluará el tiempo de ejecución para un nodo y para el resto de los nodos. De esta manera se llega a un completo estudio sobre el impacto del aumento de carga que éste propicia al sistema, para luego decidir cual es el mejor nodo de ejecución. Antes de ver esto se define:

• $N=\displaystyle\sum_{i_k\ \in\ I} r_c(i_k)\ \equiv$ es el número de unidades de procesamiento del cluster.

• $L=carga_c(t,i_k)\ \equiv$ es la carga de los elementos procesadores de cualquier nodo.

Se deduce que la carga total de todos los procesadores del cluster será 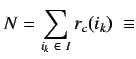$NL$ . Si la carga para cualquier nodo es $L$, la carga de los restantes es $N(L-1)$ . La carga :

• sin tener en cuenta el nuevo proceso se necesitarán $\frac{N(L-1)}{N}$ unidades de tiempo para completarse,
• con el nuevo proceso serían necesarias $\frac{NL}{N}=L$ unidades de tiempo.

La pérdida de tiempo comparativa para la ejecución de los $NL-1$ procesos en función de estas dos situaciones se puede expresar como:

$$L-\frac{1}{N}$$ .

La algorítmica de openMosix intentará minimizar esta pérdida.

Optimizando la planificación

Hasta el momento se ha estado viendo la modelización de openMosix para cada nodo, ahora sería conveniente fijar como objetivo el cálculo para el algoritmo que reconoce esta modelización y opera en consecuencia a ella. El punto de partida será el algoritmo óptimo. Esto permitirá que, tras la comparación con el que openMosix implementa, sea factible comparar resultados para ver cuánto se acerca el caso real, al ideal.

Pero la algorítmica utilizada depende enormementede la topología de los nodos el cluster, es decir, no supone el mismo esfuerzo computacional hacer los cálculos sobre efectos de carga para un conjunto de máquinas iguales^6.3 -donde la carga repercutirá numéricamente igual y por lo tanto solo será necesario hacer la predicción una vez- que para un conjunto de máquinas donde la carga supone una sobrecarga distina.

Esta situación debe tenerse en cuenta, y se modeliza de la siguiente forma:

• Nodos idénticos: todos y cada uno de los nodos del cluster poseerá todos y cada uno de los recursos de cualquier otro nodo. Esto implica que un proceso supondrá el mismo augmento de carga para cualquier nodo. Véase:

  $$IDENTICOS= \{\ \left[ R(i_a),R(i_b) \right] \ \vert \ R(i_a)=R(i... ... \wedge\ r_c(i_a)=r_c(i_b),r_m(i_a)=r_m(i_b)\ \} \Rightarrow\ c(j,i_a)=c(j,i_b)$$ .

• Nodos relacionados: todos los nodos del cluster poseen los mismos recursos, aunque pueden diferir en su ponderación. Imagínese por ejemplo un cluster de nodos idénticos aunque con los procesadores a diferentes velocidades.

  $$RELACIONADOS= \{\ \left[ R(i_a),R(i_b) \right] \ \vert \ R(i_a)... ... \neq r_c(i_b)\vee r_m(i_a)\neq r_m(i_b)\ \} \Rightarrow\ c(j,i_a)\neq c(j,i_b)$$ .

• Nodos no relacionados: los nodos tienen diferentes recursos.

  $NO\_RELACIONADOS= \{\ \left[ R(i_a),R(i_b) \right] \ \vert \ \exists\ R(i_a)\neq R(i_b)\ \ \forall\ i_a,i_b\ \in\ I\ \}$ .

Dadas estas diferentes situaciones podrá darse un algoritmo para resolver la planificación en cada una de ellas, y como se ha apuntado se medirá su ratio de competencia con el algoritmo óptimo. Por lo tanto van a compararse.

Un algoritmo que se ejecuta a la vez que los procesos -a tiempo real- es competitivo de grado $c$ si para una secuencia de entrada $I$, $algoritmo(I) \leq c\ *\ optimo(I) + \alpha$ , siendo $\alpha$ una constante definida y $optimo$ el algoritmo ideal que no se calcula.

Esta expresión toma diferentes valores para $c$ dependiendo del algoritmo utilizado para resolver la planificación, y dicha planificación depende de la topología del cluster que anteriormente ya se ha clasificado. Esta clasificación imprime diferencias a diferentes niveles. El más immediato, como se ha citado, es en la decidibilidad del algoritmo de migración. El grado de competición $c$ según la topología se define:

• Para un cluster con nodos idénticos se toma el algoritmo egoista, que asigna procesos a la máquina que tenga la menor carga en el momento de tomar la decisión de asignación de tal proceso. El ratio de competición frente al algoritmo óptimo para este algoritmo es $\rightarrow\ c=2-{\frac{1}{n}}$ .

• Para un cluster con nodos relacionados se ha implementado el algoritmo Assign-R el cual asigna cada trabajo que llega al nodo más lento. El coste de esta asignación es inferior al doble de la asignación hecha por el algoritmo óptimo, lo que da $\rightarrow\ c=2$ .

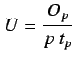• Para un cluster con nodos no relacionados no se conoce todavía un algoritmo con un ratio de competición mejor que $n$. Esto se debe a que en este caso hay que tener en cuenta muchas variables que en los demás casos podían obviarse.

  Existe no obstante el algoritmo Assign-U pensado especialmente para máquinas que no tienen relación entre sí para trabajos que se mantienen en un mismo nodo, basado en una función exponencial para el coste de un nodo en particular para una carga dada. Este algoritmo asigna cada trabajo a uno de los nodos para minimizar el coste total de todos los nodos del cluster. Este algoritmo es:

  $$U_i(j)=\alpha^{carga_i(j)+p_i(j)}-\alpha^{carga_i(j)}$$ , donde

  • $1 \leq \alpha \leq 2$ . En el caso concreto de openMosix $\alpha$ = 2.
  • $carga_i(j)$ es la carga que tiene un nodo $i$ antes de que le sea asignado un trabajo $j$ .
  • $p_i(j)$ es la carga que un trabajo $j$ añadirá a un nodo $i$ .

Como se puede ver, la formula favorece a los nodos que tienen cargas menores. Por ejemplo supongamos que tenemos 2 nodos, uno de ellos con una carga 5 y otro nodo con una carga 10. En esta configuración hemos decidido que el parámetro $\alpha$ tenga un valor de 2 (para simplificar nuestros cálculos). Se inicia un nuevo trabajo que añade una carga de 1. Para nuestros dos nodos tenemos:

$U_1(j)=2^{5+1}-2^5=64-32=32$ ,

$U_2(j)=2^{10+1}-2^{10}=2048-1024=1024$ .

Claramente el primer valor que corresponde al nodo con menor carga (5) minimiza la carga del sistema por lo tanto se elegirá el primer nodo como nodo destinatario del nuevo proceso. Las cargas de los nodos se ponderan en potencias de base 2 -gracias a $\alpha$- y esto permite agrupar los nodos con cargas iguales. La resolución del nodo con menor carga final puede calcularse a aprtir de un árbol binario. Este algoritmo es competitivo de grado $O(\log_2 n)$, para máquinas no relacionadas y trabajos permanentes.

Se puede extender este algoritmo y el ratio de competitividad a los trabajos que migran usando como máximo $O(\log_2 n)$ migraciones por trabajo. Para este nuevo tipo de situación necesitamos un parámetro más $h_i(j)$ que es la carga de un nodo $i$ justo antes de que $j$ haya sido por última vez asignado a $i$. Cuando un trabajo ha finalizado, este algoritmo comprueba la estabilidad del sistema para cada trabajo $j$ en cada nodo $M$. Esta es una condición de estabilidad que siendo $i$ el nodo donde el trabajo $j$ está actualmente, se definde como:

$$\alpha ^{h_i(j)+p_i(j)}-a^{h_i(j)}\leq 2* (\alpha^{carga_M(j)+P_M(j)}-\alpha^{carga_M(j)})$$

Si esta condición no es satisfecha por algún trabajo, el algoritmo reasigna el trabajo que no satisface la condición a un nodo $M$ que minimiza $U_M(j)$ .

Esta fórmula es quizás más omplicada de ver que las demás. Se detallan seguidamente sus factores:

Entre las reflexiones que pueden sacarse de este estudio se encuentra la explicación a la clara tendencia a construir clusters con nodos idénticos o con las mínimas diferencias entre nodos. El rendimiento será mucho más generoso.

Modelo simplificado de ponderación

Una vez formalizados los recursos, los nodos y su relación dentro del mecanismo que pone en marcha el cluster para ser capaz de realizar sus decisiones, solo falta ver la ponderación, es decir, el valor numérico que todo ello representa. La modelización que gestiona openMosix para trabajar con los elementos del cluster es un grafo poderado $G(A,V,P)$, donde:

• $A$: conjunto de arcos $a$ que se corresponden al medio de transporte de datos,
• $V$: conjunto de vértices -nodos-,
• $P$: función de incidencia del grafo, definida en $A \rightarrow V$, -se ve más adelante-.

Se define también una secuencia de llegada de peticiones, en tiempos arbitrarios, que como puede preverse son los procesos que llegan a un nodo -localmente por el usuario o desde un remoto- para ser ejecutados. Véase cada elemento con más detalle.

A cada arco -físicamente un enlace de red- se le asocia cierta ponderación que irá en aumento cada vez que se genere una comunicación sirviéndose de él. Esta situación se produce cada vez que un proceso crea un nexo entre su remote y su deputy, puesto que ambas partes deben permanecer continuamente comunicadas. Al referirse a un canal real de comunicación, es necesario asociarles una capacidad -ancho de banda-, sea $B(a)$.

La petición producida por la tarea $j$ que sea asignada a un camino -conjunto de arcos por los que circulará la petición- desde una fuente $i_s$ a un destino $i_d$ disminuye la capacidad $B(a)$ en cada uno de los arcos que pertenecen a este camino en una cantidad $carga_a(j)$. El objetivo es minimizar la congestión $C(a)$ máxima de cada uno de los enlaces, que es el ratio entre el ancho de banda requerido de un enlace y su capacidad:

$$C(a)=\frac{carga_a(j)}{B(a)}\ \equiv$$ congestión de la arista $a$ provocada por la tarea $j$

La solución viene dada por la minimización del máximo uso de procesador y memoria. Tras ello puede ser reducida a un algoritmo -en tiempo de ejecución- del problema de encaminamiento de los circuitos virtuales. Esta reducción funciona como sigue:

1. Se toman dos nodos, $i_s$ e $i_d$, y n caminos sin tramos superpuestos que tengan como origen $i_s$ y como destino el nodo $i_d$. Se considerarán únicamente los caminos que consten solamente de 2 arcos.

2. El coste desde el nodo $i_s$ hasta el $i_d$ será representado por uno de estos caminos. Los arcos se dividirán ponderando al primero de ellos con la capacidad de memoria de $i_s$, es decir $r_m(i_s)$. Al segundo de ellos se le ponderará con $r_c(i_s)$.

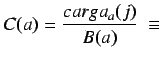Esta política acota la congestión máxima del enlace al valor máximo entre la máxima carga de procesador y el máximo uso de la memoria. De esta manera se extiende para solucionar el problema del encaminamiento.

Este algoritmo es competitivo de grado $O(\log_2 n)$. Por reducción, produce un algoritmo para manejar recursos heterogéneos que es competitivo también de grado $O(\log_2 n)$ en su máximo uso de cada recurso. Queda claro que cuando se escoge un camino se está realmente eligiendo un nodo y que las diferencias entre los dos problemas se solucionan por la función que mapea la carga de los enlaces de uno de los problemas con la carga de los recursos del otro problema. Esto hace que la forma de extender sea muy simple porque lo único que es necesario para tener en cuenta un recurso más en el sistema es añadir un arco, además de una función que mapee el problema de ese recurso en particular en el problema de encaminamiento de circuitos virtuales.

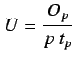La ponderación para un nodo $i_k$, poseedor de $m$ recursos consiste en una expresión que relaciona el número total de nodos $n$ del cluster con la utilización de cada recurso. La elección de los parámetros parece correcta -ha sido elegida por los desarrolladores- puesto que la parte de potencia que un nodo significa en el seno de un clsuter depende del número de nodos existentes. De igual forma un nodo potente no servirá de mucho si tiene todos sus recursos utilizados.

La expresión que se indica tendría la forma:

$$\sum_{i=1}^k f(n,u_{r_i})\ \vert \ r_i \ \epsilon\ R(i)$$ , donde $u_{r_i}$ marca la utilización del recurso $r_i$ .

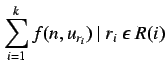Particularmente esta función de relación entre los parámetros indicados tiene la forma:

$f(n,u_{r_i})=\displaystyle\sum_{i=1}^k n^{\frac{u_{r_i}}{max[u_{r_i}]}}$, donde se relaciona para cada recurso su uso actual con su uso máximo^6.4.

NOTA: Tras estudios experimentales se ha probado que el algoritmo consegue una máxima pérdida de rendimiento dentro de $O(\log_2 n)$ de la máxima pérdida de rendimiento del algoritmo óptimo.

Esta relación entre los usos de memoria funciona tal cual para el recurso de memoria. El coste por una cierta cantidad de uso de memoria en un nodo es proporcional a la utilización de memoria -relación memoria usada/memoria total-.

Para el recurso procesador se debería saber cuál es la máxima carga posible, esto no es tan sencillo como con la memoria y va a ser necesario tener que hacer algún manejo matemático. Se asume que $L$ es el entero más pequeño en potencia de dos, mayor que la mayor carga que se haya visto hasta el momento, y que este número es la carga máxima posible. Aunque esta aproximación no sea realmente cierta sirve perfectamente para resolver el problema.

Tras estas aclaraciones las particularizaciones de ponderación para el tipo de recurso procesador y memoria quedaría respectivamente:

memoria $\rightarrow n^{\frac{u_{r_m(i)}}{r_m(i)}}$

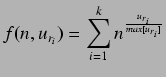y procesador $\rightarrow n^{\frac{u_{r_c(i)}}{L}}$ .